Question

If a sphere has the same volume as a cube with edge length 5, estimate the radius of the sphere.

Answer 1

Sphere's radius: approximately 3.1 units, matching volume with a cube of edge length 5 units.

The volume of a cube with edge length 5 is calculated using the formula for the volume of a cube:
`\(V_{\text{cube}} = \text{side}^3 = 5^3 = 125 \text{ cubic units}\)`.

For a sphere, the volume formula is
`\(V_{\text{sphere}} = (4)/(3) \pi r^3\)`, where r is the radius of the sphere. We're looking for a sphere with the same volume as the cube, which is 125 cubic units.

Setting up the equation
`\(125 = (4)/(3) \pi r^3\)`, we can solve for the radius \(r\).

First, rearrange the equation to solve for r³:

`\((4)/(3) \pi r^3 = 125\)\\\(r^3 = (125 * 3)/(4 \pi)\)\\\(r^3 = (375)/(4 \pi)\)`

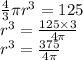
Now, solve for r by taking the cube root of both sides:

`\(r = \sqrt[3]{(375)/(4 \pi)}\)`

Approximately:

`\(r \approx \sqrt[3]{(375)/(4 \pi)} \approx \sqrt[3]{(375)/(4 * 3.14)} \approx \sqrt[3]{(375)/(12.56)} \approx \sqrt[3]{29.85}\)`

`\(r \approx 3.1\)` (rounded to one decimal place)

Hence, the estimated radius of the sphere, which has the same volume as a cube with an edge length of 5, is approximately 3.1 units.