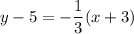Question

Write an equation in point-slope form of the line that passes through the given points, then write the equation in slope-intercept form

(-3,5). (3.3)

Answer 1

Answer:4/3 i think

Explanation:

Answer 2

Point-slope form:

`\displaystyle y-3=-(1)/(3)(x-3)`

Slope-intercept form:

`\displaystyle y=-(1)/(3)x+4`

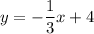
Explanation:

We want the equation in point-slope form and slope-intercept form that passes through the points (-3, 5) and (3, 3).

First, we will find the slope between the two points. By the slope formula:

`\displaystyle m=(5-3)/(-3-3)=(2)/(-6)=-(1)/(3)`

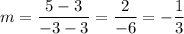
Point-slope form is given by:

`\displaystyle y-y_1=m(x-x_1)`

We can choose either point. I'm going to let (3, 3) be (x₁, y₁). The slope m is -1/3. Therefore:

`\displaystyle y-3=-(1)/(3)(x-3)`

Is the point-slope form*.

To find the slope-intercept form, we simply need to isolate y. Distribute:

`\displaystyle y-3=-(1)/(3)x+1`

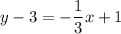
Adding 3 to both sides yields:

`\displaystyle y=-(1)/(3)x+4`

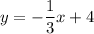
This is slope-intercept form.

*If you use the other point, the point-slope form will be:

`\displaystyle y-5=-(1)/(3)(x+3)`