Question

If the side of a square is x + 3 then the diagonal of the square is...?

A: x² + 1
B: x√2 + 3√2
C: 2x + 6
D: x²√2 + 6
E: x² + 9

Answer 1

B: x√2 + 3√2

Explanation:

`\boxed{\begin{minipage}{9 cm}\underline{Pythagoras Theorem} \\\\$a^2+b^2=c^2$\\\\where:\\ \phantom{ww}$\bullet$ $a$ and $b$ are the legs of the right triangle. \\ \phantom{ww}$\bullet$ $c$ is the hypotenuse (longest side) of the right triangle.\\\end{minipage}}`

The diagonal of a square is the hypotenuse of a right triangle with legs equal to the side length of the square.

Given:

• side length = (x + 3)

Substitute the given side length into the formula and solve for c:

`\begin{aligned}\implies c^2&=(x+3)^2+(x+3)^2\\c^2&=2(x+3)^2\\c&=√(2(x+3)^2)\\c&=√(2)√((x+3)^2)\\c&=√(2)(x+3)\\c&=x√(2)+3√(2)\end{aligned}`

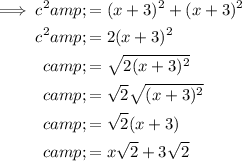
Therefore, the diagonal of the square with side length (x + 3) is:

• x√2 + 3√2