Question

Solve the system of 3 equations

Answer 1

The only point of intersection is (0, 2). This is the solution to the system of equations
`x^2 +y^2 =4, 2y=x^2 -2x+4`, and y=−x+2.

To find the points of intersection between the three equations
`x^2 +y^2 =4, 2y=x^2 -2x+4`, and y=−x+2, we can substitute the third equation into the second one and then solve the resulting system of equations.

Let's substitute y=−x+2 into
`2y=x^2 -2x+4`:

`2(-x+2)=x^2 -2x+4`

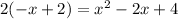
Simplify:

`-2x+4=x^2 -2x+4`

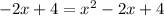
Subtract
`x^2 -2x+4` from both sides:

`0=x^2`

This implies x=0.

Now that we know x=0, we can substitute this into the third equation to find the corresponding y:

y=−x+2

y=−0+2

So, y=2.

Therefore, the only point of intersection is (0, 2). This is the solution to the system of equations
`x^2 +y^2 =4, 2y=x^2 -2x+4`, and y=−x+2.