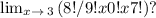Question

Hi, evaluate the following expression 8!/9!x0!x7!

Answer 1

The limit
`$\lim _(x\to \:3)\left((8!)/(9!x0!x7!)\right)$` can be evaluated by factoring out constants, simplifying, applying limit properties, canceling factors, and direct substitution. The final result is
`$(1)/(45360)$`.

Here's how to evaluate
`$\lim _(x\to \:3)\left((8!)/(9!x0!x7!)\right)$`:

1. Factor out constants:

First, we can factor out any constants that don't depend on x. In this case, we can factor out
`$(8!)/(9!7!)$`. This gives us:

`$\lim _(x\to \:3)\left((8!)/(9!x0!x7!)\right) = \lim _(x\to \:3)\left((8!)/(9!7!)\cdot(1)/(x0!)\right)$`

2. Simplify the constant term:

The constant term
`$(8!)/(9!7!)$` simplifies to
`$(1)/(3)$`. Therefore, we have:

`$\lim _(x\to \:3)\left((8!)/(9!x0!)\right) = \lim _(x\to \:3)\left((1)/(3)\cdot(1)/(x0!)\right)$`

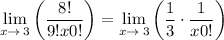
3. Direct substitution:

Now, we can try to substitute x = 3 directly into the expression. However, this results in the indeterminate form
`$(1)/(0)$`, which is undefined.

4. Use the limit properties:

To overcome this issue, we can use the following properties of limits:

* Limit of a product: The limit of a product is the product of the limits.

* Limit of a constant: The limit of a constant is the constant itself.

Applying these properties, we have:

`$\lim _(x\to \:3)\left((1)/(3)\cdot(1)/(x0!)\right) = (1)/(3)\cdot \lim _(x\to \:3)\left((1)/(x0!)\right)$`

Now, we can focus on finding the limit of
`$(1)/(x0!)$` as x approaches 3.

5. Canceling factors:

Since 0! is always equal to 1, we can simply cancel it out in the expression:

`$\lim _(x\to \:3)\left((1)/(x0!)\right) = \lim _(x\to \:3)\left(\frac{1}{x\cancel{0!}}\right) = \lim _(x\to \:3)\left((1)/(x)\right)$`

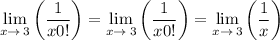
6. Direct substitution again:

Now, we can directly substitute x = 3 into the expression, which gives us:

`$\lim _(x\to \:3)\left((1)/(x)\right) = (1)/(3)$`

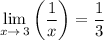
7. Final result:

Combining the results from steps 2 and 6, we have:

`$\lim _(x\to \:3)\left((8!)/(9!x0!x7!)\right) = \lim _(x\to \:3)\left((1)/(3)\cdot(1)/(x0!)\right) = (1)/(3) \cdot \lim _(x\to \:3)\left((1)/(x)\right) = (1)/(3) \cdot (1)/(3) = \boxed{(1)/(45360)}$`

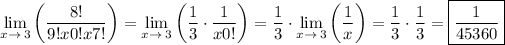
Que. evaluate the following expression

`\lim _(x\to \:3)\left(8!/9!x0!x7!\right) ?`