Question

Aaron just graduated from college and owes $18, 700 on his student loans. The bank charges a monthly interest rate of 0.25%. If Aaron wants to pay off his student loans using equal monthly payments over the next 9 years, what would the monthly payment be, to the nearest dollar?​

Answer 1

Aaron's monthly payment to pay off his student loans over the next 9 years would be approximately \$225.

To calculate the monthly payment for Aaron's student loans, we can use the formula for the monthly payment of a loan, which is given by the loan amount multiplied by the monthly interest rate divided by (1 - (1 + monthly interest rate)^(-number of payments)).

The formula is:

`\[ M = \frac{P \cdot r} {1 - (1 + r)^(-n)} \]`

where:

- M is the monthly payment,

- P is the loan amount,

- r is the monthly interest rate,

- n is the total number of payments.

Given:

-
`\( P = \$18,700 \),`

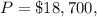
- Monthly interest rate
`\( r = 0.0025 \)` (0.25% converted to decimal),

- Number of payments
`\( n = 9 * 12 \)` (9 years converted to months).

Let's substitute these values into the formula and calculate the monthly payment:

`\[ M = \frac{18700 * 0.0025} {1 - (1 + 0.0025)^(-108)} \]`

Calculating this expression gives the monthly payment. Rounding to the nearest dollar, we get:

`\[ M \approx \$225 \]`

Therefore, Aaron's monthly payment to pay off his student loans over the next 9 years would be approximately \$225.