Answer:
1) h = 7.8 yards
2) t = 23.8 feet
Explanation:
Question 1
In a right-angled triangle, the sine of an angle is defined as the ratio of the length of the side opposite that angle to the length of the hypotenuse.

In the given right triangle:
- Angle = 15°
- Side opposite the angle = h
- Hypotenuse = 30 yards
Therefore, to find the vertical distance (h), we can use the sine ratio:
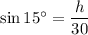
Solve for h:
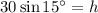
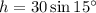
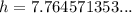
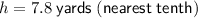
So, the vertical distance (h) is 7.8 yards (rounded to the nearest tenth).

Question 2
In a right-angled triangle, the tangent of an angle is defined as the ratio of the length of the side opposite that angle to the length of the side adjacent that angle.

In the given right triangle:
- Angle = 50°
- Side opposite the angle = t
- Side adajcent the angle = 20 feet
Therefore, to find the height of the tree (t), we can use the tangent ratio:
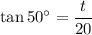
Solve for t:
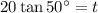
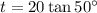
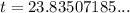
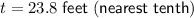
So, the height of the tree (t) is 23.8 feet (rounded to the nearest tenth).