The triangles are both marked with the single-tick congruency mark on two sides. This means that they not only share two sides but are also both isosceles. They also share the center side, so, by SSS congruency, these triangles are congruent and thus share all 3 angles. If they share all 3 angles, however, the shape they form together is a parallelogram. If it is a parallelogram, we can use the alternate interior angles theorem, so, the angle adjacent to angle 1 is also 26°. If these are isosceles triangles, the angles that lie on the non-congruent side are congruent, so angle 1 and the angle adjacent to the given angle are congruent. So, since all angles in a triangle add up to 180°:
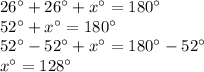
So, the measure of angle 2 is 128°