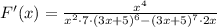The expression
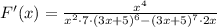 when simplified would be
when simplified would be
![\[F'(x) = (x^3)/((3x + 5)^6 \cdot (x - 10)).\]](https://img.qammunity.org/2024/formulas/mathematics/college/j81mox0q1ayshob6tnrzkb69gt2yrihjpe.png)
To solve the expression
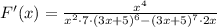 , let's simplify the expression step by step.
, let's simplify the expression step by step.
First, factor out common terms:
![\[F'(x) = (x^4)/((3x + 5)^6 \cdot (x^2 \cdot 7 - (3x + 5) \cdot 2x)).\]](https://img.qammunity.org/2024/formulas/mathematics/college/nx458ciwaz9lhc0v6hcdm4s0twks1591rx.png)
Now, simplify the denominator:
![\[F'(x) = (x^4)/((3x + 5)^6 \cdot (7x^2 - 6x^2 - 10x)).\]](https://img.qammunity.org/2024/formulas/mathematics/college/ln90gahegyx1cfsswq2n56bb12aserhm9p.png)
Combine like terms:
![\[F'(x) = (x^4)/((3x + 5)^6 \cdot (x^2 - 10x)).\]](https://img.qammunity.org/2024/formulas/mathematics/college/3kxctsimleb2gdxo09jkyjizhg8hkymyv9.png)
Factor out \(x\) from the denominator:
![\[F'(x) = (x^4)/(x \cdot (3x + 5)^6 \cdot x(x - 10)).\]](https://img.qammunity.org/2024/formulas/mathematics/college/lsne7ufmngijoufzo3ir9kc6vhj36l05ml.png)
Simplify further:
![\[F'(x) = (x^3)/((3x + 5)^6 \cdot (x - 10)).\]](https://img.qammunity.org/2024/formulas/mathematics/college/j81mox0q1ayshob6tnrzkb69gt2yrihjpe.png)
This is the simplified form of the given expression F'(x).
The question probable may be:
Simplify the given expression :