Function has a point of inflection at x=2, is concave up for x<2 and concave down for x>2, leading to a maximum value at x=2.
The polynomial function
has an increasing rate of change for
.
The rate of change of
is decreasing for
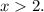
Relate rate of change to concavity
A function's rate of change is represented by its first derivative, denoted as
.
An increasing rate of change indicates a positive second derivative, meaning the function is concave up.
A decreasing rate of change indicates a negative second derivative, meaning the function is concave down .
Analyze behavior at x = 2
Since the rate of change is increasing for
, we know
for
. This implies the function is concave up.
Similarly, as the rate of change decreases for
, we know
for
. This implies the function is concave down.
The transition from concave up to concave down occurs at
. This point is called a point of inflection .
Differentiate between minimum and maximum
The graph of
is rising before x = 2 because the rate of change is positive.
After x = 2, the rate of change becomes negative, indicating the function starts to fall.
Therefore, the function reaches its maximum value at x = 2.
complete the question
For the polynomial function \(g\), the rate of change of \(g\) is increasing for \(x < 2\) and decreasing for \(x > 2\). Considering this, which statement regarding the behavior of the function \(g\) at \(x = 2\) is most likely to be true?
1. The graph of \(g\) has a minimum at \(x = 2\).
2. The graph of \(g\) has a maximum at \(x = 2\).
3. The graph of \(g\) is concave down for \(x < 2\) and concave up for \(x > 2\).
4. The graph of \(g\) has a point of inflection at \(x = 2\), being concave up for \(x < 2\) and concave down for \(x > 2\).