In the first triangle with sides 3 cm, 4 cm, and 5 cm, trigonometric ratios for angles A and B are
 . In the second triangle, ratios are
. In the second triangle, ratios are
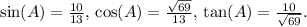
Let's use the Pythagorean Theorem to find the missing side in each right triangle and then determine the trigonometric ratios for angles A and B.
### Part a:
Given right triangle ACB with BC = 3 cm and AC = 4 cm.
Using the Pythagorean Theorem:

![\[AB^2 = 4^2 + 3^2\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/r33lpng8lmd6gjy43lt1jd06c4vfme30zl.png)
![\[AB^2 = 16 + 9\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/nflb5pa5ileyu1ky51yy1lheanuvgaqc71.png)
![\[AB^2 = 25\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/mkzo8i45k446wm5p2h2ubarueatebuoti6.png)
AB = 5
Now, we have all three sides of the triangle: AC = 4 cm, BC = 3 cm, and AB = 5 cm.
The trigonometric ratios for angle A and B are as follows:
- For angle A:
-
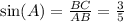
-
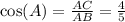
-
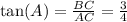
- For angle B (since it's a right triangle,
 are the same as for angle A).
are the same as for angle A).
### Part b:
Given right triangle ACB with BC = 10 cm and AB = 13 cm.
Using the Pythagorean Theorem:

![\[AC^2 = 13^2 - 10^2\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ob7ku8jfdyuqwkbvh3ryxlg2xcnt37h5bx.png)
![\[AC^2 = 169 - 100\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/k8t59tu8khyek2ab3ahh811djcn7ijzq5x.png)
![\[AC^2 = 69\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/7hlsyuc9c479p1xh6zoxayjxrhc98buksd.png)
![\[AC = √(69)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/hj4metoomrujkq0fwpfhti95dy7ds6vui6.png)
Now, we have all three sides of the triangle: AC =
 cm, BC = 10 cm, and AB = 13 cm.
cm, BC = 10 cm, and AB = 13 cm.
The trigonometric ratios for angle A and B are as follows:
- For angle A:
-
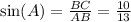
-
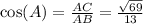
-
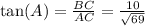
- For angle B (since it's a right triangle,
 are the same as for angle A).
are the same as for angle A).