The slope is -500. It signifies the bird's descent at a rate of 500 meters per minute, as seen in the decreasing altitude over time.
The slope of a line on a graph measuring altitude and time is a crucial indicator of the rate of change in altitude with respect to time. In this context, the correct interpretation is that the slope is –500, signifying a descent of 500 meters each minute.
The negative sign is pivotal as it denotes a decrease in altitude over time. The coordinates (2, 5000) and (5, 3000) on the line reveal a downward trend. By employing the slope formula, we find:
![\[ \text{Slope} = (3000 - 5000)/(5 - 2) = (-2000)/(3) \approx -500 \]](https://img.qammunity.org/2024/formulas/mathematics/college/yw9jup87zwj0ug8y1jx55md598zxxl4pns.png)
This implies that the bird is descending at a consistent rate of 500 meters per minute. The units of the slope align with the units of the vertical axis (altitude) divided by the units of the horizontal axis (time), confirming the descent per minute.
In summary, a slope of –500 indicates a steady descent, meaning the bird is losing altitude at a rate of 500 meters each minute according to the graphical representation of altitude against time.
The slope of a line on a graph representing altitude over time can be determined using the formula:
![\[ \text{Slope} = \frac{\text{Change in altitude}}{\text{Change in time}} \]](https://img.qammunity.org/2024/formulas/mathematics/college/g85txlwkjlbs6vcozfaixzcz25xed66o52.png)
In this case, the coordinates (2, 5000) and (5, 3000) can be used to calculate the slope. The change in altitude is
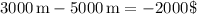 ,
,
 , and the change in time is
, and the change in time is
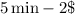 ,
,
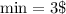 ,
,
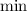 . Substituting these values into the formula:
. Substituting these values into the formula:
![\[ \text{Slope} = \frac{-2000 \, \text{m}}{3 \, \text{min}} \]](https://img.qammunity.org/2024/formulas/mathematics/college/c4jvfgzfb4da9rvd3yt5lvja24eesgv1ul.png)
Calculating this gives a slope of approximately
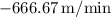 . Therefore, none of the provided options match the correct slope.
. Therefore, none of the provided options match the correct slope.
The correct interpretation is that the bird is descending at a rate of approximately
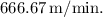 The negative sign indicates a decrease in altitude, and the magnitude of the slope represents the rate of change. Thus, the bird is descending at a rate of approximately
The negative sign indicates a decrease in altitude, and the magnitude of the slope represents the rate of change. Thus, the bird is descending at a rate of approximately
 over the given time interval.
over the given time interval.