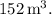The volume of the composite figure is
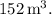
To find the volume of the composite figure, you need to calculate the volume of the rectangular prism and then subtract the volume of the removed cube.
1. Volume of the rectangular prism:
![\[ V_{\text{prism}} = \text{length} * \text{width} * \text{height} \]](https://img.qammunity.org/2024/formulas/mathematics/college/t09xe2uh1jiv9h9lp64vjpo1k6tohqlilz.png)
![\[ V_{\text{prism}} = 9 \, \text{m} * 8 \, \text{m} * 3 \, \text{m} \]](https://img.qammunity.org/2024/formulas/mathematics/college/idkf8ss4ov7asgv2n89aj6cylpr6xaa3pv.png)
![\[ V_{\text{prism}} = 216 \, \text{m}^3 \]](https://img.qammunity.org/2024/formulas/mathematics/college/p1hjeqc8lahi3ufpgtunhakbqhrjs1o26y.png)
2. Volume of the cube:
![\[ V_{\text{cube}} = \text{side}^3 \]](https://img.qammunity.org/2024/formulas/mathematics/college/wlf664vy8ucooijiz0e7jzf1x6t6j6l1l0.png)
![\[ V_{\text{cube}} = 4 \, \text{m} * 4 \, \text{m} * 4 \, \text{m} \]](https://img.qammunity.org/2024/formulas/mathematics/college/paexau6ljkrj9770t3uiy4myuni6dig9bi.png)
![\[ V_{\text{cube}} = 64 \, \text{m}^3 \]](https://img.qammunity.org/2024/formulas/mathematics/college/100nzs8c9du5oeqnitg7ep3izrabdqleny.png)
Now, subtract the volume of the cube from the volume of the prism to get the volume of the composite figure:
![\[ \text{Volume of composite figure} = V_{\text{prism}} - V_{\text{cube}} \]](https://img.qammunity.org/2024/formulas/mathematics/college/33qfrnt06biub1722s85hkecmx4e7zhz9w.png)
![\[ \text{Volume of composite figure} = 216 \, \text{m}^3 - 64 \, \text{m}^3 \]](https://img.qammunity.org/2024/formulas/mathematics/college/rga2a9j0l75j6kuihvvhg20dacxidj23yr.png)
![\[ \text{Volume of composite figure} = 152 \, \text{m}^3 \]](https://img.qammunity.org/2024/formulas/mathematics/college/nrnys2tixwcx21wmppwkjbi52nt3yig9lz.png)
Therefore, the volume of the composite figure is