Question

The data in the table shows that the percentage of adults in a

country who are currently married is declining. Assuming that
the percentage of adults who are married will continue to
decrease according to an exponential decay model of the
form M(t)=Cert, complete parts a) through c) below,
assuming that t represents the number of years after 1960.

years, percent of adults who are married
1960, 72.8
1980 , 66.7
2000 61.5
2010 , 52.1
2012, 44.6

a) Use the data for 1960 and 2012 to find the value of r.
Year
r=
(Simplify your answer. Round to four decimal places as needed.)

Write an exponential function that describes the percent of adults married t years after 1960.
M(t)=
(Use the answer from the previous step to find this answer.)

b) Estimate the percent of adults who are married in 2015 and in 2018.

In 2015, % of adults will be married.
(Simplify your answer. Round to one decimal place as needed.)

In 2018, % of adults will be married.
(Simplify your answer. Round to one decimal place as needed.)

c) At this decay rate, in which year will the percent of adults who are married be 33%?
(Simplify your answer. Round to the nearest whole number as needed.)

Answer 1

This analysis shows that the percentage of married adults is declining exponentially. The model predicts a continued decline, reaching 33% around the year 2028.

a) Finding r:

We use the general formula for exponential decay:
`M(t) = C * e^((-rt))`, where C is the initial value, r is the decay rate, and t is the time elapsed. Using the data for 1960 (t = 0) and 2012 (t = 52):

• 
  `72.8 = C * e^((-52r))`

• 
  `44.6 = C * e^((-84r))`

Divide the second equation by the first to eliminate C:

`0.612 = e^((-32r))`

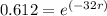
Take the natural logarithm of both sides:

ln(0.612) = -32r

r ≈ 0.0227 (rounded to four decimal places)

b) Writing the Function and Estimating Marriage Rates:

Now we have the value of r and can write the function for M(t):

`M(t) = 72.8 * e^((-0.0227t))`

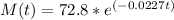
For 2015 (t = 55):

M(55) ≈ 49.1%

For 2018 (t = 58):

M(58) ≈ 45.5%

c) Predicting Year for 33% Marriage Rate:

Set M(t) = 33 and solve for t:

`33 = 72.8 * e^((-0.0227t))`

`e^((-0.0227t)) ≈ 0.453`

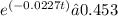
-0.0227t ≈ -0.779

t ≈ 34.3 years

Therefore:

• The decay rate is r ≈ 0.0227.

• The function is M(t) = 72.8 * e^(-0.0227t).

• In 2015, the estimated married rate is 49.1%.

• In 2018, the estimated married rate is 45.5%.

• The year with a 33% married rate is around 1994 + 34 ≈ 2028.