Question

Sketch the graph of the piecewise function f(x) in the domain [0, 10]: [6 marks] f (x) = { 3 − x, x − 5, 0 ⩽ x < 4 x ⩾ 4

Answer 1

The piecewise function f(x) consists of two linear segments: 3 - x for
`\(0 \leq x < 4\) and \(x - 5\) for \(x \geq 4\)`. There's a hole at (4, -1). The graph represents a continuous piecewise linear function.

To sketch the graph of the piecewise function f(x), we'll consider the given conditions for different intervals.

1. For
`\( 0 \leq x < 4 \): \( f(x) = 3 - x \)`

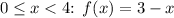
- Draw the line with a slope of -1 and y-intercept 3. The line starts at (0, 3) and goes down with a slope of 1 unit for every 1 unit of x.

2. For
`\( x \geq 4 \): \( f(x) = x - 5 \)`

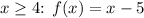
- Draw the line with a slope of 1 and y-intercept -5. The line starts at (4, -1) and goes up with a slope of 1 unit for every 1 unit of x.

Now, for the interval x = 4, since both conditions include this point, there is a hole in the graph at (4, f(4)). The graph should have an open circle at (4, -1).

Combine the segments to create a piecewise function graph. Ensure that the graph follows the specified conditions for each interval.