Question

Solve for X.
I have been on this question for a bit i am unsure if I am correct.

Answer 1

Using the Intercept Theorem in triangles AMN and ABC, with MN parallel to BC, the value of x is found to be 16. The theorem establishes a proportion, leading to the equation 2x-5 = 27, solving to x = 16.

In a situation where MN is parallel to BC and AM is a transversal, we can apply the similarity criterion known as the Intercept Theorem. According to this theorem, if a pair of parallel lines is intersected by a transversal, the ratio of the lengths of the segments they are divided into is the same for both lines.

In
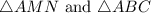`\(\triangle AMN\) and \(\triangle ABC\)`, we can use the Intercept Theorem to set up the following proportion:

`\[(AM)/(AB) = (AN)/(AC)\]`

Substitute the given values:

`\[(2x-5)/((x+8) + (20)) = (22.5)/(22.5 + 20)\]`

Now, solve for x:

`\[2x-5 = (22.5 \cdot 48)/(42.5) = 27\]`

2x = 27 + 5

2x = 32

x = 16

So, the value of x is 16.