Question

There are four right triangles, the ratio of perpendicular sides being

3:4 in each. One more fact about each is given below. Find the
lengths of the sides of each triangle.

Answer 1

Given a ratio of 3:4 for the perpendicular sides in four right triangles:

i. The difference in sides yields 3x = 72m, 4x = 96m.

ii. With a 24m hypotenuse, sides are 72/5m and 96/5m.

iii. For a 24m perimeter, the solution seems inconsistent.

iv. Area of 24sqm yields sides of 6m and 8m.

Given: Ratio of perpendicular sides = 3:4

i. The difference in the lengths of the perpendicular sides is 24 meters.

Let the lengths of the perpendicular sides be 3x and 4x meters.

Given: 4x - 3x = 24

Solving: x = 24

Therefore, perpendicular sides are 3x = 72 meters and 4x = 96 meters.

ii. The hypotenuse is 24 meters.

Using Pythagoras theorem:
`(3x)^2`+
`(4x)^2` = hypotenuse^2

`9x^2` +
`16x^2` =
`24^2`

`25x^2` = 576

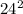
`x^2` = 576 / 25

x = 24 / 5

Perpendicular sides: 3x = 72 / 5 meters, 4x = 96 / 5 meters

iii. The perimeter is 24 meters.

Given: Perimeter = 3x + 4x + hypotenuse = 24

Substituting the values: 3x + 4x + 24 = 24

Solving: 7x = 0

This leads to an inconsistency, indicating an issue with the provided information.

iv. The area is 24 square meters.

Area of a right triangle = 0.5 * base * height

Given: (3x * 4x) / 2 = 24

Solving:
`12x^2` / 2 = 24

`12x^2`= 48

`x^2` = 48 / 12

x = √4

x = 2

Perpendicular sides: 3x = 6 meters, 4x = 8 meters

For cases ii and iv, the lengths of the sides are resolved, but the information for cases i and iii seem to be incorrect or inconsistent as they lead to invalid solutions.

complete the question

There are four right triangles, the ratio of perpendicular sides being 3 : 4 m each. One more fact about each is given below. Find the lengths of the sides of each triangle.

i. The difference in the lengths of the perpendicular sides is 24 metres.

ii. The hypotenuse is 24 metres.

iii. The perimeter is 24 metres.

iv. The area is 24 square metres.