Question

Find a polynomial f(x) of degree 4 with real coefficients and the following zeros. - 1 (multiplicity 2), 1 3i

Answer 1

The polynomial f(x) with the given zeros and real coefficients is
`x^4 -4x^3 +24x^2 -40x+100.`

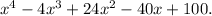
If the polynomial has real coefficients and the complex root 1+3i, then its conjugate 1−3i must also be a root due to the complex conjugate theorem.

So, the zeros are: −1 (multiplicity 2), 1+3i, and 1−3i.

The factors corresponding to these zeros are
`(x+1)^2` (for the −1 with multiplicity 2) and

`(x-(1+3i))(x-(1-3i))=((x-1)-3i)((x-1)+3i)`for the complex conjugate pair.

Let's expand the factors to obtain the polynomial:

`(x+1)^2 ((x-1)-3i)((x-1)+3i)\\(x+1)^2 ((x-1)^2 -(3i)^2\\(x+1)^2 ((x-1)^2 +9)`

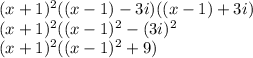
Now, let's multiply and simplify:

`(x+1)^2 (x^2 -2x+1+9)\\(x+1)^2 (x^2 -2x+10)`

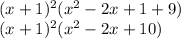
Expanding further:

`x^2 (x^2 -2x+10)-2x(x^2 -2x+10)+10(x^2 -2x+10)\\x^4 -2x^3 +10x^2 -2x^3 +4x^2 -20x+10x^2 -20x+100\\x^4 -4x^3 +24x^2 -40x+100`

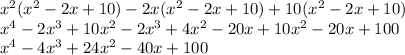
So, the polynomial f(x) with the given zeros and real coefficients is
`x^4`
`-4x^3 +24x^2 -40x+100.`

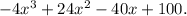
Question

Find a polynomial f(x) of degree 4 with real coefficients and the following zeros. - 1 (multiplicity 2), 1 +3i