Question

4. Lenny says, 14 Explain what he has done incorrectly and work out the correct answer.​

Answer 1

Lenny incorrectly added fractions with denominators 11 and 3 without finding a common denominator. The correct sum, with a common denominator of 33, is
`\((43)/(3)\).`

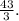
Lenny has incorrectly added fractions by denominators. To add fractions, you need a common denominator. In this case, the common denominator would be the least common multiple (LCM) of 11 and 3, which is 33.

Here's the correct process:

`\[ (7)/(11) + (2)/(3) \]`

Now, we need to make the denominators the same. Multiply the first fraction by
`\((3)/(3)\)` and the second fraction by
`\((11)/(11)\)` to get a common denominator of 33.

`\[ (7 \cdot 3)/(11 \cdot 3) + (2 \cdot 11)/(3 \cdot 11) \]`

Simplify the fractions:

`\[ (21)/(33) + (22)/(33) \]`

Now that the denominators are the same, add the numerators:

`\[ (21 + 22)/(33) \]`

`\[ (43)/(33) \]`

Finally, simplify the fraction:

`\[ (43)/(33) = (43)/(3 \cdot 11) = (43)/(3) \]`

So, the correct answer is
`\((43)/(3)\).`

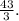
The probable question may be:

Lenny says 7/11 + 2/3 = 9/14 Explain what he has done incorrectly and work out the correct answer.