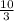Answer:
see explanation
Explanation:
To solve a quadratic equation , it must be in the form
ax² + bx + c = 0 ( a ≠ 0 )
given
3x² - 4x = 20 ( subtract 20 from both sides )
3x² - 4x - 20 = 0 , then
a = 3 , b = - 4 , c = - 20
This is the principal error in the given solution
c= 20, instead of c = - 20 ← ***
In that, by inserting incorrect value for c, the formula gives the incorrect solution.
The solution can be obtained by factorising the equation
Consider the factors of the product of the coefficient of the x² term and the constant term which sum to give the coefficient of the x- term
product = 3 × - 20 = - 60 and sum = - 4
the factors are + 6 and - 10
use these factors to split the x- term
3x² + 6x - 10x - 20 = 0 ( factor the first/second and third/fourth terms )
3x(x + 2) - 10(x + 2) = 0 ← factor out (x + 2) from each term
(x + 2)(3x - 10) = 0 ← in factored form
equate each factor to zero and solve for x
x + 2 = 0 ⇒ x = - 2
3x - 10 = 0 ⇒ 3x = 10 ⇒ x =
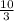
The solutions to the equation are x = - 2 , x =