Question

Hello! If anyone can help me with this that would be much appreciated. ^_^​

Answer 1

5 meters

Step-by-step explanation:

In the given scenario, the length of the pendulum corresponds to the radius of the circle formed by its swing, and the angle through which it swings corresponds to the central angle.

Therefore, to determine the length of the pendulum, we can use the arc length formula:

`\boxed{\begin{array}{l}\underline{\textsf{Arc length}}\\\\s= (\theta\pi r)/(180^(\circ))\\\\\textsf{where:}\\\phantom{ww}\bullet\;\textsf{$s$ is the arc length.}\\\phantom{ww}\bullet\;\textsf{$r$ is the radius.}\\\phantom{ww}\bullet\;\textsf{$\theta$ is the central angle in degrees.}\end{array}}`

In this case:

• s = 5 m
• θ = 60°

Substitute the given values into the formula and solve for r:

`5=(60^(\circ)\cdot \pi \cdot r)/(180^(\circ))`

`5=(\pi r)/(3)`

`15=\pi r`

`r=(15)/(\pi)`

`r=4.7746482927...`

`r=5\; \sf meters\;(nearest\;whole\;number)`

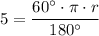
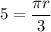
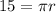
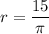
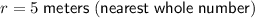
Therefore, the length of the pendulum is 5 meters (rounded to the nearest whole number).