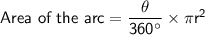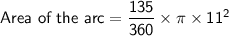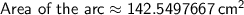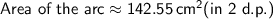Answer:
1) a) 4.28in b) 14.97in²
2) a) 39.09m b) 156.38m²
3) a) 25.92cm b) 142.55cm²
Explanation:
1. For the first scenario:
 ,
,
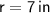
Length of the arc:
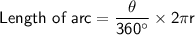
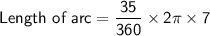
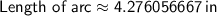
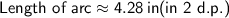
Area of the arc:
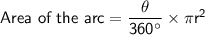
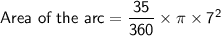
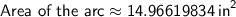
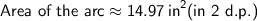
2. For the second scenario:
 ,
,
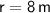
Length of the arc:
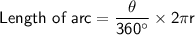
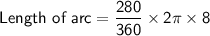
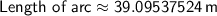
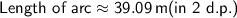
Area of the arc:
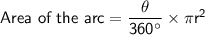
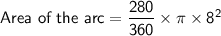
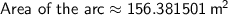
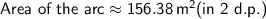
3. For the third scenario:
 ,
,
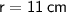
Length of the arc:
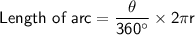
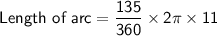
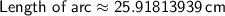
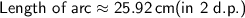
Area of the arc: