Question

a) Using Pythagoras' theorem, work out which of the triangles below, if any, are right-angled. b) Write a sentence to explain your answer. 10 cm N Triangle XYZ 35 cm 34 cm 15 cm W Triangle UVW 36 cm 39 cm Not drawn accurately​

Answer 1

Neither Triangle XYZ nor Triangle UVW is a right-angled triangle based on Pythagoras' theorem.

To determine if a triangle is right-angled using Pythagoras' theorem, you check if the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. In a right-angled triangle, this equation holds true.

Let's consider Triangle XYZ with sides 35 cm, 34 cm, and 15 cm. According to Pythagoras' theorem:

`c^(2) = a^(2) + b^(2)`

For Triangle XYZ:

`35^(2) = 34^(2) + 15^(2)`

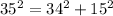
1125 = 1156 + 225

1125 =/ 1381

The equation is not true, so Triangle XYZ is not a right-angled triangle.

Now, let's consider Triangle UVW with sides 36 cm, 39 cm, and 10 cm:

`36^(2) = 39^(2) + 10^(2)`

1296= 1521 +100

1296=/1621

Similarly, the equation is not true for Triangle UVW.

Therefore, neither Triangle XYZ nor Triangle UVW is a right-angled triangle based on Pythagoras' theorem.