Question

Hi please help 100 points, no links or wrong answers

Answer 1

In both cases, the sum of given angles is B+C or A+B, and they are less than 180°, so these problems do not represent the ambiguous case.

Let's solve the first triangle ABC with the given information:

B=71°, C=22°, and a=5.20

We can use the Law of Sines to find the missing angles and sides:

`(sinA)/(a)` =
`(sin B)/(b)` =
`(sin C)/(c)`

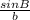Substitute the given values:

`(sinA)/(5.20)` =
`(sin 71)/(b)` =
`(sin 22)/(c)`

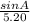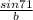Now, we can find b using the angle B:

b =
`(5.20.sin71)/(sinA)`

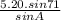
Next, we can find c using the angle C:

c =
`(5.20. sin22)/(sin A)`

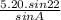
Lastly, we can find angle A using the fact that the sum of angles in a triangle is 180°:

A=180°−B−C

Now, let's solve the second triangle ABC with the given information:

A=35°, a=11, and b=7

We can use the Law of Sines again to find the missing angles and sides:

`(sinA)/(a)` =
`(sin B)/(b)` =
`(sin C)/(c)`

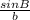Substitute the given values:

`(sin 35)/(11)` =
`(sin B)/(7)` =
`(sin C)/(c)`

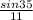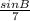Now, find B using b:

B =
`sin^(-1)` (
`(7 sin 35)/(11)` )

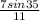Next, find C using c:

C =
`sin^(-1)` (
`(7 sin 35)/(c)` )

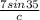To check if the problem is the ambiguous case, we need to ensure that the sum of given angles is less than 180°.

In both cases, the sum of given angles is B+C or A+B, and they are less than 180°, so these problems do not represent the ambiguous case.