Question

Find the velocity, acceleration, and speed of a particle with the given position function. r(t) = (6 cos(t), 5t, 6 sin(t)) V(B) = |(-6 sin(t),5,6 cos(t)) a(t) = (-6 cos(t),0, – 6 sin(t)) |v(e)=

Answer 1

To find the velocity, acceleration, and speed of a particle, differentiate the position function to get the velocity and acceleration, then find the magnitude of the velocity to get the speed.

Step-by-step explanation:

To find the velocity, acceleration, and speed of a particle with the given position function, we can use the formulas for velocity and acceleration:

V(t) = dr(t)/dt

`a(t) = d^2r(t)/dt^2`

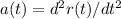
For the given position function r(t) = (6 cos(t), 5t, 6 sin(t)), we can differentiate it to find the velocity and acceleration:

V(t) = (-6 sin(t), 5, 6 cos(t))

a(t) = (-6 cos(t), 0, -6 sin(t))

The speed of the particle is the magnitude of the velocity vector:

speed = |V(t)|

=
`|-6 sin(t)|^2 + |5|^2 + |6 cos(t)|^2`

=
`36 sin^2(t) + 25 + 36 cos^2(t)`

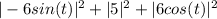
= 61