Question

find the volume of the solid whose base is in the first quadrant(s) bounded by y=18−2x2 and the x-axis using square cross-sections perpendicular to the x-axis. enter answer using exact values.

Answer 1

The exact volume of the solid is 999.

To find the volume of the solid with a base in the first quadrant bounded by
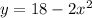`\(y = 18 - 2x^2\)` and the x-axis, using square cross-sections perpendicular to the x-axis, we can set up the integral:

`\[ V = \int_(a)^(b) (18 - 2x^2)^2 \, dx \]`

First, find the x-values where
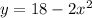`\(y = 18 - 2x^2\)` intersects the x-axis:

`\[ 18 - 2x^2 = 0 \]`

Solving for x, we get
`\(x = \pm 3\)`.

Since we're dealing with the first quadrant, choose a = 0 and b = 3.

Now, substitute these values into the integral:

`\[ V = \int_(0)^(3) (18 - 2x^2)^2 \, dx \]`

Simplify the integrand:

`\[ V = \int_(0)^(3) (324 - 72x^2 + 4x^4) \, dx \]`

Now, integrate term by term:

`\[ V = \left[ 324x - 24x^3 + (4)/(5)x^5 \right]_(0)^(3) \]`

Evaluate at x = 3 and x = 0:

`\[ V = (972 - 216 + 243) - 0 = 999 \]`

Thus, the exact volume of the solid is 999.