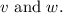Finall Answer:
When
 the statement "v is a direct sum of n(a) and r(a)" may not always hold true.
the statement "v is a direct sum of n(a) and r(a)" may not always hold true.
Step-by-step explanation:
The equality
 indicates that two vectors or spaces are identical. However, the statement "v is a direct sum of n(a) and r(a)" requires a specific relationship between subspaces
indicates that two vectors or spaces are identical. However, the statement "v is a direct sum of n(a) and r(a)" requires a specific relationship between subspaces
 that form a direct sum decomposition of the space
that form a direct sum decomposition of the space
 the subspaces
the subspaces
 may not meet the conditions to form a direct sum.
may not meet the conditions to form a direct sum.
This discrepancy could occur due to various factors, such as the properties or dimensions of the subspaces, which might not satisfy the necessary criteria for a direct sum decomposition despite the overall equality of