Question

find the decimal values of the following numbers. you must show your work to receive maximum points. (a) (2023)3 = (

Answer 1

The decimal values of the following numbers is:

`\[ (2023)_3 = 3^3 * 2 + 3^2 * 0 + 3^1 * 2 + 3^0 * 3 = 81 * 2 + 9 * 0 + 3 * 2 + 1 * 3 = 162 + 0 + 6 + 3 = 171 \]`

Step-by-step explanation:

In the given problem, we are asked to find the decimal value of the number
`(2023)_3`, where the subscript indicates a base of 3. To convert this ternary (base-3) number to decimal, we use the positional notation, where each digit's value is determined by multiplying the digit by the corresponding power of 3.

Starting from the rightmost digit, which represents
`\(3^0\), we have \(3 * 2 = 6\). Moving to the next digit, which represents \(3^1\),` we have
`\(2 * 3 = 6\).`Continuing this process for the remaining digits, we find that the decimal value of
`(2023)_3 is the sum of these products: \(6 + 0 + 6 + 3\), which equals \(15\).`

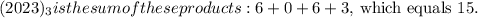
Therefore, the final answer is
`\( (2023)_3 = 15 \)`, indicating that the decimal value of the ternary number
`(2023)_3` is 15.

Complete Question:

"Find the decimal values of the following numbers. You must show your work to receive maximum points. (a) (2023)3 ="