Question

Tom wants to call Lilly but he is not sure about the last digit in the phone number. He just remembers it was one of the numbers 1, 4, 7, 9. He decides to try all four numbers (in order) as the last digit until Lilly picks up the phone: If X is the number of trials (until success), what is the pmf for X?

a) px(x) = 1/4, x = 1,2,3,4
b) px(x) = (3/4)ˣ⁻¹, x = 1,2,3,4
c) px(x) = (1/4)(3/4)⁴⁻ˣ , x = 1,2,3,4
d) px(x) = (3/4)ˣ⁻¹(1/2)²⁻ˣ , x = 1,2,3,4
e) px(x) = (1/4)(3/4)⁴⁻ˣ , x = 1,2,3
f) px(x) = (1/4)(3/4)ˣ⁻¹ , x = 1,2,3,4
g) px(x) = (3/4)ˣ⁻¹(1/4)⁴⁻ˣ , x = 1,2,3
h) px(x) = 3/4, x = 1,2,3,4

Answer 1

The probability mass function for the number of trials until Tom dials Lilly's correct phone number is geometrically distributed, with px(x) =
`(3/4)^(x-1) * (1/4)` for x = 1, 2, 3, 4.

Step-by-step explanation:

When Tom is trying different numbers for the last digit of Lilly's phone number with four options (1, 4, 7, or 9), and assuming each number is equally likely, we are dealing with a geometric distribution scenario where trials are conducted until a success is achieved. The probability mass function (pmf) of X, where X is the number of trials until success, is
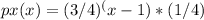`px(x) = (3/4)^(x-1) * (1/4)`, for x = 1, 2, 3, 4. This is because with each trial there is a 3/4 chance that he dials the wrong number and a 1/4 chance that he dials the correct number.

Note: The probability distribution function must satisfy two conditions: the sum of all probabilities must equal one, P(x = 1) + P(x = 2) + P(x = 3) + P(x = 4) = 1, and each individual probability, P(x), must be between 0 and 1.