Final Answer:
The integral is:
![\[ \int x \ln(x) \,dx = (x^2)/(2) \ln(x) - (x^2)/(4) + C \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/3t09ja6rg85i0c8cpjr86d1g8vgci0zitt.png)
Step-by-step explanation:
To solve the given integral, let's first make the substitution
 . Now, the integral becomes
. Now, the integral becomes
 Substituting back in terms of
Substituting back in terms of
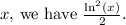
Next, use integration by parts with
 accordingly. Applying the integration by parts formula
accordingly. Applying the integration by parts formula
 we get the expression
we get the expression
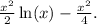
Therefore, the final answer is
 is the constant of integration. This result combines the outcomes of the substitution and integration by parts, providing a concise expression for the original integral.
is the constant of integration. This result combines the outcomes of the substitution and integration by parts, providing a concise expression for the original integral.