Question

SUFFICIENT STATISTICS

How many distinct combinations of letters from this expression can exist?

Answer 1

There are 58,595,845 distinct combinations of letters from the expression "SUFFICIENT STATISTICS."

To find the number of distinct combinations of letters from the expression "SUFFICIENT STATISTICS," we can use combinatorics. The expression contains repeated letters, so we'll use the multinomial coefficient to account for the repeated occurrences of certain letters

The expression "SUFFICIENT STATISTICS" has 19 letters in total. Here's the breakdown of the letters:

5 'S's

3 'I's

2 'U's

2 'F's

2 'C's

2 'T's

1 'E'

1 'N'

1 'T'

The formula for the multinomial coefficient is given by:

`\left[\begin{array}{ccc}n\\n_(1) ,n_(2)....,n_(k) \\\end{array}\right]` =
`(n!)/(n!_(1) ,n!_(2)....,n!_(k))`

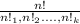
where n is the total number of items, and
`n_(1) ,n_(2),.....,n_(k)` are the counts of each distinct item.

For "SUFFICIENT STATISTICS," the number of distinct combinations is

`\left[\begin{array}{ccc}19\\5 ,3,2,2,2,2,1,1,1,1 \\\end{array}\right]` =
`(19!)/(5!,3!,2!,2!,2!,2!,1!,1!,1!,1! )` =
`(19!)/(5760)` = 58,595,845

So, there are 58,595,845 distinct combinations of letters from the expression "SUFFICIENT STATISTICS."