By definite integrals, the area of the region is equal to 625 square units.
How to determine the area between the two curves
In this problem we must determine the area between two curves by definite integrals. First, determine the points of intersection of the two curves:
4 · x³ = 100 · x
4 · x³ - 100 · x = 0
4 · x · (x² - 25) = 0
4 · x · (x + 5) · (x - 5) = 0
x = 0 or x = - 5 or x = 5
y = 100 · 0
y = 0
y = 100 · (- 5)
y = - 500
y = 100 · 5
y = 500
Third, determine the area between the two curves: (f(x) = 100 · x, g(x) = 4 · x³)
![I = \int\limits^0_(-5) {[g(x) - f(x)]} \, dx + \int\limits^5_0 {[f(x) - g(x)]} \, dx](https://img.qammunity.org/2024/formulas/mathematics/high-school/wyd4r0thjg2nmi9k6p04uqfq6kocky2txt.png)
![I = \int\limits^0_(- 5) {[4\cdot x^3-100\cdot x]} \, dx + \int\limits^5_0 {[100\cdot x - 4\cdot x^3]} \, dx](https://img.qammunity.org/2024/formulas/mathematics/high-school/c1gy5xoym945g0upyoiwbpjomhbndqk5zc.png)
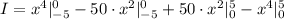
I = 0⁴ - (- 5)⁴ - 50 · 0² + 50 · (- 5)² + 50 · 5² - 50 · 0² - 5⁴ + 0⁴
I = 0 - 625 + 0 + 1250 + 1250 - 0 - 625 + 0
I = 625 + 625
I = 1250