Final Answer:
The integrating factor is μ(t) =
 , and the general solution to the differential equation y' + 3y =
, and the general solution to the differential equation y' + 3y =
 is given by y(t) = c *
is given by y(t) = c *
 + (1/3) * t *
+ (1/3) * t *
 , where c is the constant of integration.
, where c is the constant of integration.
Step-by-step explanation:
To solve the given first-order linear differential equation y' + 3y =
 we can use an integrating factor μ(t). The integrating factor is calculated using the coefficient of y, which is 3 in this case. The integrating factor (μ(t)) is given by the formula μ(t) =
we can use an integrating factor μ(t). The integrating factor is calculated using the coefficient of y, which is 3 in this case. The integrating factor (μ(t)) is given by the formula μ(t) =
 .
.
Now, multiply both sides of the differential equation by the integrating factor μ(t):
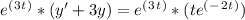
This simplifies to d/dt (e^(3t) * y) = te^(t). Integrate both sides with respect to t:
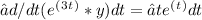
The left side integrates to
 * y, and the right side integrates to (1/3) * t *
* y, and the right side integrates to (1/3) * t *
 + c, where c is the constant of integration. Therefore,
+ c, where c is the constant of integration. Therefore,
 * y = (1/3) * t *
* y = (1/3) * t *
 + c.
+ c.
Solving for y, we get y(t) = c *
 + (1/3) * t *
+ (1/3) * t *
 which is the general solution to the given differential equation. The constant c is determined by the initial conditions if provided. This solution describes the family of curves that satisfy the given differential equation.
which is the general solution to the given differential equation. The constant c is determined by the initial conditions if provided. This solution describes the family of curves that satisfy the given differential equation.