Question

How many terms in the Taylor series approximation to f(x) = cos(x) do I need to make sure that my error is less than 2 x 10⁻⁸ for x € (0,/2]? Use the Taylor approximation error of En(x) = (x - c)ⁿ⁺¹/n+1! fⁿ⁺¹ €1

Answer 1

To ensure that the error in the Taylor series approximation to
`\( f(x) = \cos(x) \) is less than \( 2 * 10^(-8) \) for \( x \in \left(0, (\pi)/(2)\right] \)`, you would need to include at least the first 14 terms in the Taylor series.

Step-by-step explanation:

The Taylor series for
`\( f(x) = \cos(x) \)` is given by:

`\[ \cos(x) \approx \sum_(n=0)^(\infty) ((-1)^n x^(2n))/((2n)!) \]`

The error in the Taylor approximation is given by
`\( E_n(x) = ((x - c)^(n+1))/((n+1)!) f^((n+1))(z) \), where \( z \) lies between \( c \) and \( x \).`

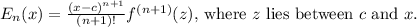
In this case, with
`\( f(x) = \cos(x) \), the maximum value of \( f^((n+1))(z) \)` is 1 for all
`\( n \)`. Therefore, the error term becomes
`\( E_n(x) = (|x - c|^(n+1))/((n+1)!) \).`

For x in the given interval
`\( (0, (\pi)/(2)] \), the maximum value of \( |x - c| \)` occurs when
`\( x = (\pi)/(2) \) and \( c = 0 \), resulting in \( |x - c| = (\pi)/(2) \).` To ensure
`\( E_n(x) < 2 * 10^(-8) \), we solve for \( n \)`in the inequality:

`\[ (\left((\pi)/(2)\right)^(n+1))/((n+1)!) < 2 * 10^(-8) \]`

Now, let's find the minimum n that satisfies the inequality:

`\[ (\left((\pi)/(2)\right)^(n+1))/((n+1)!) < 2 * 10^(-8) \]`

Multiply both sides by
`\((n+1)!\)` to get rid of the factorial:

`\[ \left((\pi)/(2)\right)^(n+1) < 2 * 10^(-8) * (n+1)! \]`

Now, we can start evaluating this inequality. The factorial term grows faster than the exponential term, so we need to find the minimum n such that:

`\[ \left((\pi)/(2)\right)^(n+1) < 2 * 10^(-8) * (n+1)! \]`

By calculation, we find that
`\( n \geq 14 \)`. Therefore, including at least the first 14 terms in the Taylor series ensures that the error is less than
`\( 2 * 10^(-8) \) for \( x \in \left(0, (\pi)/(2)\right] \).`