Final Answer:
If
 , then
, then
 .
.
Step-by-step explanation:
Let's start by understanding the given property
 . This implies that elements in
. This implies that elements in
 but not in
but not in
 are the same as elements in
are the same as elements in
 . Mathematically, this can be expressed as
. Mathematically, this can be expressed as
 , where
, where
 represents the complement of set
represents the complement of set
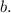
Now, let's analyze the implications of this equality. If
 , it means that the elements exclusive to
, it means that the elements exclusive to
 are the same as the elements exclusive to
are the same as the elements exclusive to
 . In other words, the sets
. In other words, the sets
 have identical elements outside their intersection.
have identical elements outside their intersection.
If
 and
and
 have the same elements outside their intersection, it implies that every element in
have the same elements outside their intersection, it implies that every element in
 is also in
is also in
 and vice versa. Therefore,
and vice versa. Therefore,
 and
and
 are equal, and we can conclude that if
are equal, and we can conclude that if
 , then
, then

In summary, the given property ensures that the elements exclusive to each set are the same, leading to the conclusion that the sets themselves are identical. This establishes the proof that if
 , then
, then
