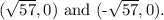Question

Find the foci and vertices of the conic section. 249−264=36

Answer 1

The conic section represented by the equation 249−264=36 is an ellipse. The foci of the ellipse are at (√21, 0) and (-√21, 0), and the vertices are at (√57, 0) and (-√57, 0).

Step-by-step explanation:

The given equation represents an ellipse, which is a conic section defined by the difference of the distances between two fixed points (foci) and any point on the ellipse being constant. To find the foci and vertices, let's first rewrite the equation in standard form for an ellipse:

`\[ ((x-h)^2)/(a^2) + (y^2)/(b^2) = 1 \]`

Comparing this with the given equation, we have (a² = 21) and (b² = 36). The major axis is along the x-axis, so a is the square root of the larger denominator, and before is the square root of the smaller denominator. Therefore,
`\(a = √(21)\)`and
`\(b = √(36) = 6\).` The center of the ellipse, denoted by (h, k), is(0, 0) in this case.

The foci are located at
`\((\pm √(a^2 - b^2), 0)\).` Substituting the values, we find the foci at
`\((√(21), 0)\) and \((- √(21), 0)\).` The vertices are given by (pm a, 0), so the vertices are at
`\((√(21), 0)\) and \((- √(21), 0)\)`. Therefore, the final answer is that the foci are at (\(\sqrt{21}, 0)\) and (-\(\sqrt{21}, 0)\), and the vertices are at
`(\(√(57), 0)\) and (-\(√(57), 0)\).`