Final Answer:
The maximum value of
 such that
such that
 whenever
whenever
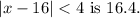
Step-by-step explanation:
The given inequality
 implies that
implies that
 .
.
The second inequality
 can be broken down into two separate inequalities:
can be broken down into two separate inequalities:
 ,
,
which simplify to
 , respectively.
, respectively.
Combining these conditions, we find that
 must be less than
must be less than
 and satisfy
and satisfy
 . Therefore, the maximum value of
. Therefore, the maximum value of
 that satisfies these conditions is
that satisfies these conditions is
 .
.