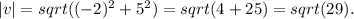Final answer:
The component form of vector u is (3, -2), and its magnitude is √13. The component form of vector v is (-2, 5), and its magnitude is √29.
Step-by-step explanation:
To find the component form and magnitude of the vector given by u = (3,-2) and v = (-2,5), we first need to understand that the component form of a vector is simply the vector itself, which is expressed as an ordered pair (x, y) in two-dimensional space. Hence, for vector u, the component form is (3, -2), and for vector v, the component form is (-2, 5).
The magnitude (or length) of a vector w = (x, y) can be found using the formula
 . Therefore, the magnitude of vector u is
. Therefore, the magnitude of vector u is
 , and the magnitude of vector v is
, and the magnitude of vector v is