Question

Find explicit particular solutions of the initial value problem.
(dy/dx)=ye^(x), y(0)=2e

Answer 1

The solution to the given initial value problem is a particular solution of the differential equation
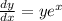`\((dy)/(dx) = ye^x\)` with the initial condition
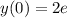`\(y(0) = 2e\)`. After solving the differential equation, the explicit particular solution is
`\(y(x) = 2e^(e^x)\)`.

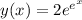Explanation:

The given initial value problem involves solving the first-order linear ordinary differential equation
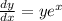`\((dy)/(dx) = ye^x\)`, where
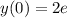`\(y(0) = 2e\)` is the initial condition. To find the particular solution, we integrate the equation with respect to (x).

The integration process involves isolating variables and manipulating the terms to solve for (y). After the integration, we obtain the general solution. However, to find the particular solution that satisfies the initial condition, we substitute (x = 0) into the general solution and solve for the constant.

In this specific case, the solution to the differential equation is
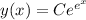`\(y(x) = Ce^(e^x)\)`, where (C) is the constant of integration. By substituting
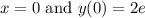`\(x = 0\) and \(y(0) = 2e\)`, we can solve for (C), leading to (C = 2). Substituting this value back into the general solution, we arrive at the explicit particular solution
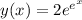`\(y(x) = 2e^(e^x)\)`. This exponential form signifies the growth of the solution as (x) increases, emphasizing the dynamic nature of the differential equation.