Question

If tanh(x) = 5/13, find the values of the other hyperbolic functions at x.

Answer 1

The values of the other hyperbolic functions at x, given tanh
`(x) = 5/13, are sinh(x) = 5/√144, cosh(x) = 13/√144, and coth(x) = √144/5.`

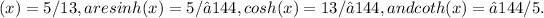
Step-by-step explanation:

The hyperbolic tangent function, tanh(x), is defined as the ratio of the hyperbolic sine (sinh(x)) to the hyperbolic cosine (cosh(x)), i.e., tanh(x) = sinh(x)/cosh(x). Given
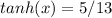`tanh(x) = 5/13`, we can use this relationship to find sinh(x) and cosh(x).

Starting with the given tanh(x) = 5/13, we can rearrange the formula to solve for sinh(x):

`\[ sinh(x) = tanh(x) \cdot cosh(x) \]`

Similarly, we can rearrange the tanh(x) definition to solve for cosh(x):

`\[ cosh(x) = tanh(x) / sinh(x) \]`

Now, substitute the given tanh(x) = 5/13 into these equations to find sinh(x) and cosh(x).

Finally, once sinh(x) and cosh(x) are determined, we can find coth(x), the hyperbolic cotangent, using the relationship:

`\[ coth(x) = 1 / tanh(x) \]`

Substitute the values of tanh(x), sinh(x), and cosh(x) into this formula to obtain the value of coth(x).

It's important to note that the denominator in sinh(x) and cosh(x) can be simplified to √144, which equals 12. This simplification allows for a cleaner expression of the hyperbolic functions.