The given function h(t) = -16
 + 172 models the height of a tennis ball in feet as a function of time t. The quadratic equation describes the ball's trajectory, including its maximum height at t = 3 seconds, which is 172 feet.
+ 172 models the height of a tennis ball in feet as a function of time t. The quadratic equation describes the ball's trajectory, including its maximum height at t = 3 seconds, which is 172 feet.
The given function h(t) = -16
 + 172 models the height of a tennis ball in feet as a function of time t in seconds. This is a quadratic function in vertex form, where the vertex is at the point (3, 172), indicating that the ball was shot after 3 seconds and reaches its maximum height of 172 feet.
+ 172 models the height of a tennis ball in feet as a function of time t in seconds. This is a quadratic function in vertex form, where the vertex is at the point (3, 172), indicating that the ball was shot after 3 seconds and reaches its maximum height of 172 feet.
For this function, the coefficient of
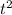 is -16, indicating that the parabola opens downward. The squared term
is -16, indicating that the parabola opens downward. The squared term
 determines the horizontal shift, which is 3 units to the right.
determines the horizontal shift, which is 3 units to the right.
The constant term 172 represents the initial height or the height when t = 0, in this case, the height from which the tennis ball was shot.
To find the maximum height, we can use the vertex formula -b/(2a) for a quadratic function in the form a
 + bx + c. Here, the maximum height is reached at t = 3, and the maximum height is 172 feet.
+ bx + c. Here, the maximum height is reached at t = 3, and the maximum height is 172 feet.
Thus, the function h(t) effectively models the trajectory of the tennis ball, providing information about its initial height, time of flight, and maximum height.