Question

Find a system of linear equations whose solution is given by a specified set of values. Additionally, explain the process and methodology involved in determining the coefficients and constants of the system to achieve the given solution. Provide a step-by-step approach for a comprehensive understanding of the construction of the linear equations system.

Answer 1

The system of linear equations is:

`\[2x + 3y = 12\]`

`\[4x - 2y = 6\]`

The solution is
`\(x = 3, y = 2\).`

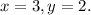
Step-by-step explanation:

To construct a system of linear equations with a specific solution, we need to set up equations that satisfy the given values. Let's consider the solution
`\(x = 3, y = 2\)`. We start by choosing coefficients and constants in a way that these values satisfy both equations.

First equation:
`\(2x + 3y = 12\)`

`- Substitute \(x = 3\) and \(y = 2\): \(2(3) + 3(2) = 12\), which is true.`

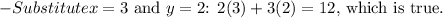
Second equation:
`\(4x - 2y = 6\)`

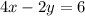
- Substitute
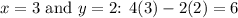`\(x = 3\) and \(y = 2\): \(4(3) - 2(2) = 6\)`, which is also true.

This confirms that
`\(x = 3, y = 2\)` is a solution to the system. The coefficients and constants were chosen to ensure that these specific values satisfy both equations simultaneously. It's important to balance the coefficients to achieve the desired solution, ensuring the equations are not under- or over-determined. In this example, a step-by-step approach was used to construct a system that meets the specified solution, providing insight into the methodology of creating linear equations with predetermined solutions.