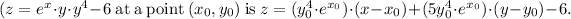Final answer
The equation of the tangent plane to
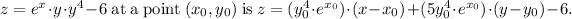
Explanation
To find the equation of the tangent plane to the given surface
 we first determine its partial derivatives with respect to \(x\) and \(y\). Then, using the point
we first determine its partial derivatives with respect to \(x\) and \(y\). Then, using the point
 where the tangent plane is to be found, substitute these values into the partial derivatives to compute the slope of the tangent plane at that point. The equation of a plane in point-normal form is
where the tangent plane is to be found, substitute these values into the partial derivatives to compute the slope of the tangent plane at that point. The equation of a plane in point-normal form is
 where \(A\) and \(B\) represent the partial derivatives evaluated at
where \(A\) and \(B\) represent the partial derivatives evaluated at
 Thus, after calculating the partial derivatives and evaluating them at the given point, the equation of the tangent plane can be expressed as
Thus, after calculating the partial derivatives and evaluating them at the given point, the equation of the tangent plane can be expressed as
 This equation represents the tangent plane to the surface at the specified point.
This equation represents the tangent plane to the surface at the specified point.
The equation of the tangent plane to \