Final Answer:
The matrix-vector products are as follows:
1.
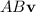 is undefined.
is undefined.
2.
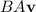 is defined.
is defined.
Step-by-step explanation:
The product
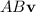 is undefined because the number of columns in matrix (A) (denoted as
is undefined because the number of columns in matrix (A) (denoted as
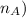 must be equal to the number of rows in matrix (B) (denoted as
must be equal to the number of rows in matrix (B) (denoted as
 )) for the product (AB) to be defined.
)) for the product (AB) to be defined.
In this case, if (A) is an
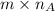 matrix and (B) is a
matrix and (B) is a
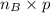 matrix, the product (AB) is only defined if
matrix, the product (AB) is only defined if
 . In the given question, the vector
. In the given question, the vector
 is of size
is of size
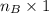 . However, since (A) and (B) have different numbers of columns
. However, since (A) and (B) have different numbers of columns
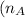 and
and
 the product
the product
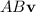 cannot be computed.
cannot be computed.
On the other hand, the product
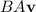 is defined. In this case, matrix (B) has
is defined. In this case, matrix (B) has
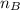 columns, and matrix (A) has
columns, and matrix (A) has
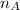 columns. Therefore, the product (BA) is defined, resulting in a matrix of size
columns. Therefore, the product (BA) is defined, resulting in a matrix of size
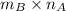 . Multiplying this matrix by the vector
. Multiplying this matrix by the vector
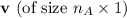 yields a vector of size
yields a vector of size
 , and the product is well-defined.
, and the product is well-defined.
In summary, the product
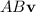 is undefined due to a mismatch in the number of columns between matrices (A) and (B), while the product
is undefined due to a mismatch in the number of columns between matrices (A) and (B), while the product
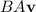 is defined since the matrices (B) and (A) satisfy the necessary conditions for multiplication.
is defined since the matrices (B) and (A) satisfy the necessary conditions for multiplication.