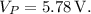Final Answer:
The electric potential at a point P, located in the xy-plane, due to point charges
 and
and

Step-by-step explanation:
The electric potential
 at point P is the sum of the potentials
at point P is the sum of the potentials
 and
and
 due to
due to
 and
and
 respectively. The potential
respectively. The potential
 at P due to
at P due to
 is given by Coulomb's law:
is given by Coulomb's law:
 where
where
 is Coulomb's constant,
is Coulomb's constant,
 is the charge, and
is the charge, and
 is the distance from
is the distance from
 to P. Similarly,
to P. Similarly,
 at P due to
at P due to
 is given by
is given by
 , where
, where
 is the charge, and
is the charge, and
 is the distance from
is the distance from
 to P.
to P.
The distances
 can be calculated using the distance formula
can be calculated using the distance formula
 , where
, where
 and
and
 are the coordinates of the charges. Substituting the values, we find
are the coordinates of the charges. Substituting the values, we find
 and
and
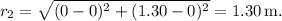
Finally, we can find the total potential
 by summing
by summing
 . Substituting the known values, we get
. Substituting the known values, we get
 . Plugging in the numbers, we find
. Plugging in the numbers, we find