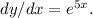Final answer:
If the differential equation is actually meant to be
 , then after integrating both sides, applying the natural logarithm, and simplifying, the correct solution is option d
, then after integrating both sides, applying the natural logarithm, and simplifying, the correct solution is option d
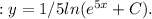
Step-by-step explanation:
To solve the differential equation
 , we need to separate variables and integrate. However, if this is an error and the actual equation is
, we need to separate variables and integrate. However, if this is an error and the actual equation is
 which is separable, or potentially
which is separable, or potentially
 which could be solved via separation of variables, we can find the solution presented in the student's options.
which could be solved via separation of variables, we can find the solution presented in the student's options.
If the equation is
 , we would integrate both sides with respect to x to obtain:
, we would integrate both sides with respect to x to obtain:
Applying the natural logarithm, we get:
Hence, option d,
 would be correct if the differential equation is
would be correct if the differential equation is