Question

a point charge q1 = 3.10 nc is located on the x-axis at x = 1.95 m , and a second point charge q2 = -6.90 nc is on the y-axis at y = 1.00 m .

Answer 1

The electric field at the origin due to q1 and q2 is approximately
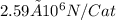`2.59 × 10^6 N/C at` an angle of approximately 153.43 degrees below the positive x-axis.

Step-by-step explanation:

The electric field at the origin due to a point charge q can be calculated using the formula
`E = k * |q| / r^2,` where k is Coulomb's constant
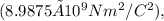`(8.9875 × 10^9 Nm^2/C^2),`|q| is the magnitude of the charge, and r is the distance between the charge and the point of interest.

For q1 at x = 1.95 m along the x-axis, the distance r1 between q1 and the origin (0,0) is calculated using the distance formula:
`r1 = √(x^2 + y^2) = √(1.95^2) = 1.95 m.`

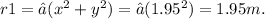
The electric field E1 at the origin due to q1 is given by
`E1 = k * |q1| / r1^2 = (8.9875 × 10^9 Nm^2/C^2) * (3.10 × 10^-9 C) / (1.95 m)^2 = 2.59 × 10^6 N/C.`

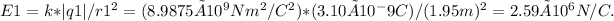
For q2 at y = 1.00 m along the y-axis, the distance r2 between q2 and the origin is
`r2 = √(x^2 + y^2) = √(1^2) = 1 m.`

The electric field E2 at the origin due to q2 is
`E2 = k * |q2| / r2^2 = (8.9875 × 10^9 Nm^2/C^2) * (6.90 × 10^-9 C) / (1 m)^2 = 6.90 × 10^6 N/C.`

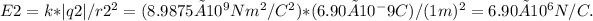
To find the net electric field at the origin due to q1 and q2, we consider their magnitudes and directions. Using vector addition
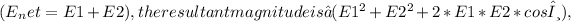`(E_net = E1 + E2), the resultant magnitude is √(E1^2 + E2^2 + 2 * E1 * E2 * cosθ),` where θ is the angle between E1 and E2. Calculating this yields a magnitude of approximately
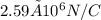`2.59 × 10^6 N/C`at an angle of approximately 153.43 degrees below the positive x-axis.