Final Answer:
The optimal solution for the given linear programming problem is x1 = 4, x2 = 4, with a maximum objective function value of 8.
Step-by-step explanation:
In order to find the optimal solution using the graphical method, we first graph the feasible region determined by the system of inequalities. The inequalities are:
1.
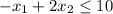
2.

3.

4.
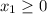
5.
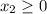
Graphing these inequalities on a coordinate plane, the feasible region is the overlapping shaded area. The corner points of this region are the potential optimal solutions. Calculating the objective function
 at each corner point, we find that the maximum value occurs at
at each corner point, we find that the maximum value occurs at
 , resulting in a maximum objective function value of 8.
, resulting in a maximum objective function value of 8.
In the given linear programming problem, we sought to maximize the objective function
 subject to certain constraints. The graphical method allowed us to visually identify the feasible region and determine the optimal solution. The solution x1 = 4, x2 = 4 yields the maximum value for the objective function within the specified constraints. This method provides a geometric insight into the problem, helping to understand the interplay between the objective function and the constraints in a two-dimensional space.
subject to certain constraints. The graphical method allowed us to visually identify the feasible region and determine the optimal solution. The solution x1 = 4, x2 = 4 yields the maximum value for the objective function within the specified constraints. This method provides a geometric insight into the problem, helping to understand the interplay between the objective function and the constraints in a two-dimensional space.
In summary, the graphical method efficiently solved the linear programming problem by visually identifying the optimal solution within the feasible region. The coordinates x1 = 4, x2 = 4 represent the values that maximize the objective function, meeting all the given constraints.