Question

What is the electric force on a proton 2.3 fm from the surface of the nucleus? Hint: Treat the spherical nucleus as a point charge.

Answer 1

The electric force on a proton 2.3 femtometers (fm) from the surface of the nucleus, treating the nucleus as a point charge, can be calculated using Coulomb's law and is
`\[F = (k \cdot |q_1 \cdot q_2|)/(r^2)\]`, where
`\(F\)` is the force,
`\(k\)` is Coulomb's constant,
`\(q_1\) and \(q_2\)` are charges (proton's charge and the nucleus's charge, respectively), and
`\(r\)` is the separation distance.

Explanation:

Utilizing Coulomb's law
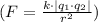`(\(F = (k \cdot |q_1 \cdot q_2|)/(r^2)\))`, where
`\(k\)` is Coulomb's constant
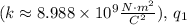`(\(k \approx 8.988 * 10^9 (N \cdot m^2)/(C^2)\)), \(q_1\)`represents the charge of the proton
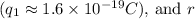`(\(q_1 \approx 1.6 * 10^(-19) C\)), and \(r\)` is the distance from the proton to the nucleus's surface (given as
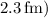`\(2.3 \, \text{fm}\))`. Assuming the nucleus as a point charge
`\(q_2\)`, the force can be calculated.

Substituting the known values into Coulomb's law yields:

`\[F = ((8.988 * 10^9 (N \cdot m^2)/(C^2)) \cdot |(1.6 * 10^(-19) C) \cdot q_2|)/((2.3 * 10^(-15) m)^2)\]`

The value of
`\(q_2\)` (charge of the nucleus) needs to be known or provided to precisely calculate the electric force acting on the proton at a distance of 2.3 femtometers from the nucleus's surface. Coulomb's law determines the force between charged particles, and in this case, the force on the proton depends on the charge of the nucleus, which is assumed to be concentrated at the nucleus's center. Therefore, knowledge of the nucleus's charge is crucial for an accurate calculation of the electric force acting on the proton at the specified distance.