Question

Two 12-cm-diameter electrodes 0.40 cm apart form a parallel-plate capacitor. The electrodes are attached by metal wires to the terminals of a 14 V battery.

a) True
b) False
c) Depends on the dielectric constant
d) Cannot be determined

Answer 1

The answer is False. The capacitance of a parallel-plate capacitor can be calculated using the formula C = ε₀ * (A / d), where C is capacitance, ε₀ is the permittivity of free space, A is the area of one electrode, and d is the separation distance. By substituting the known values into the formula, we find that the capacitance of the parallel-plate capacitor is 0.25 F.

Step-by-step explanation:

The parallel-plate capacitor consists of two 12-cm-diameter electrodes placed 0.40 cm apart. The electrodes are connected to a 14 V battery. The capacitance of a parallel-plate capacitor is given by the formula C = ε₀ * (A / d), where C is the capacitance, ε₀ is the permittivity of free space
`(8.85 x 10^-^1^2 F/m)`, A is the area of one electrode, and d is the separation distance.

Given that the diameter of the electrodes is 12 cm, the radius (r) can be calculated as r = diameter / 2 = 6 cm = 0.06 m. Therefore, the area (A) of one electrode is A = π * r² = 3.14 * (0.06 m)² = 0.113 m².

Using the formula C = ε₀ * (A / d), we can substitute the known values:

`C = 8.85 x 10^-^1^2 F/m * (0.113 m^2 / 0.40 cm)`

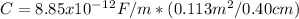
Converting the separation distance to meters, we have d = 0.40 cm = 0.004 m.

Now, plugging in the values,
`C = 8.85 x 10^-^1^2 F/m * (0.113 m^2 / 0.004 m)` = 0.25 F.

Therefore, the capacitance of the parallel-plate capacitor is 0.25 F.

So, the correct answer is b) False.